物理 第三部:流体の物理
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,力を受けると容易に変形する流体に関連し, 【流体とは】, 【流体の分類】, 【流体力学とは】, 【静止流体の圧力】, 流体静力学の基本の【アルキメデスの原理】, 【パスカルの原理】, 【ボイルの法則】 に項目を分けて紹介する。
【流体とは】
少しの力を加えると容易に変形する気体(gas)や液体(liquid)などの物質を一般に流体(fluid)という。
後述するように,流体が静止している場合は,接線応力(tangential stress)が働かず,垂直応力(normal stress)として圧力のみが作用するので,流体を“静止状態において接線応力の発生しない連続体の総称”とも定義できる。
流体は,構成する原子や分子の位置が固定されている剛体(固体)と異なり,原子や分子の位置が容易に変わる。このため,剛体とは異なる特徴が多く,流体における力のつりあい,運動の関係などを議論する学問分野(流体力学)として独立している。
流体と力
流体が静止しているとき
流体内部では,任意の面に対して常に垂直の方向に力が作用する(パスカルの原理)。すなわち,流体内部で任意の面に向かう単面積当たりの力(応力)として,法線応力(normal stress)ともいわれる垂直応力(normal stress)で押し合う場合の圧力(pressure)に限定され,接線方向のせん断応力や張力はなどの接線応力(tangential stress)が作用しない。
流体が運動するとき
ある面に垂直に作用する垂直応力の他に,流体の内部摩擦により,面と平行(接線方向)な接線応力が現れる。
接線応力は,せん断応力とも呼ばれ,この応力が現れる現象を粘性といい,発生した力を粘性応力ともいう。
運動するときの垂直応力は,対象とする面の両側から押し合う場合の圧力の他に引っ張り合う場合の張力(tension)も発生する。
圧力の単位
1971年の国際度量衡総会で,1 m2 当たり 1 N (ニュートン)の力が加わった場合の圧力の SI 単位を,ブレーズ・パスカルに因んで 1 Pa (パスカル)と定められた。
SI 単位が定められる以前から,気圧の表示などに bar(バール),atm (気圧),mmHg (水銀柱ミリメートル),Torr(トール)などの圧力を示す歴史的な単位が長く用いられ,技術分野によっては今現在も用いている。これらの概要については圧力分類と単位で紹介する。
【参考:基礎用語】
- 流体力学(fluid mechanics , hydrodynamics)
静止状態や運動状態の流体に働く力などの性質,流体中の物体に及ぼす力などを論じる力学の部門。流体力学では電気的に中性で電離していない流体のみを扱い,電離した流体は流体力学とは別分野とされるプラズマ物理学で扱われる。 - 応力(stress)
工学分野でで頻繁に用いられる用語で,物体に外部から力が作用するとき,その反作用として物体内に生ずる分布内力をいう。
応力には,応力ベクトルと応力テンソルがあり,単に応力という場合は,応力テンソルを指すことが多い。 - 応力テンソル(stress tensor)
物体内部の微小面の法線と力の作用方向が一致する垂直応力成分,一致しないせん断応力成分の2種類に分類することができる。 - 垂直応力(normal stress)
法線応力ともいわれ,物体内部のある面の垂直方向に作用する応力をいう。 - 圧力(pressure)
垂直応力が押し合う場合,すなわち,物体の表面あるいは内部の任意の面に向かい垂直に押す単面積当たりの力をいう。 - 張力(tension)
垂直応力が引き合う場合,すなわち,物体のある平面に垂直方向に作用する引っ張り合う単位面積当たりの力をいうが,一般的には,単に引っ張る力の意味で用いることも少なくないので,単位を記すなど文脈において,単位面積当たりの力(応力)なのか外力としての引く力かを明確にしておくと誤解を避けられる。 - 接線応力(tangential stress)
ずれ応力,せん断応力ともいわれ,物体のある面を境にずれが起こるとき,それに対応して物体内部に生じる力。 - せん断応力(shear stress)
せん断応力(剪断応力)は,接線応力やシャー応力ともいわれ,物体内部のある面に平行方向に作用する応力,すなわち面がすべるように作用する応力をいう。 - ダイラタント流体(Dilatant Fluid)
流れが強く(速度勾配が大きい)なるほど剪断応力が増加し流れにくくなる流体。 - 擬塑性流体(pseudoplastic fluid)
流れが強く(速度勾配が大きい)なるほど剪断応力の増加が減少し流れやすくなる流体。 - ビンガム流体(Bingham Plastic)
一定の剪断応力に達しないと流動を始めない流体。 - 物質の三態(three states of matter)
物質の状態,固体,液体,気体をまとめて物質の三態や三相と呼ぶ。三態が安定的に共存する温度を三重点という。 - 水理学(hydraulics)
水の動力学的性質を研究する流体力学の一分野で,ダム,河川,港湾,上下水道などを扱う土木工学では水理学,ポンプ,タービン,プロペラ,潤滑などを扱う機械工学では水力学(hydromechanics)と呼ぶことが多い。 - 方向余弦(direction cosine)
空間に直交座標系(x,y,z)があるとき,有向直線(ベクトル)が X ,Y ,Z 軸の正の向きとの“はさむ角”をそれぞれα,β,γとすると,l = cos α,m = cosβ,n = cosγをその直線の方向余弦という。 - 理想気体(ideal gas)
理想気体は,完全気体( perfect gas )ともいい,現実には存在しない理想的な気体である。すなわち,ボイル=シャルルの法則を状態方程式とし,内部エネルギーは体積によらず温度だけの関数となり,断熱変化に対してポアソンの法則に従う。 このためには,気体を構成する粒子(分子や原子など)の体積と,粒子間の相互作用をともに無視できる系として扱われる。 - 熱力学的温度(thermodynamic temperature)
一般的には絶対温度(absolute temperature)と呼ばれることが多い。イギリスの物理学者,初代ケルビン男爵がカルノーサイクル(温度の異なる 2 つの熱源の間で動作する可逆熱サイクル)で出入りするエネルギーから温度目盛を構築できることを提唱したことから始まる。
熱力学的温度は,カルノーサイクルの効率が1となる温度(これ以上冷やせない温度)を基準とする温度で,この基準の温度に到達するには無限の仕事が必要となるので,この温度を絶対零度( 0 K ,-273.15 ℃)という。
温度の単位は,ケルビン( K )を用いる。温度目盛の間隔は,セルシウス度と同じ,即ち 1 K = 1 ℃である。
現在は,物質量の比により厳密に定義(国際度量衡委員会)された同位体組成を持つ水の三重点( triple point : 0.01 ℃ ,273.16 K )の熱力学温度の 1/273.16 を 1 ケルビン( K )と定義している。
ページの先頭へ
【流体の分類】
一般に実在の流体は,運動した際に接線応力が発生するので粘性流体(viscous fluid)と呼ばれるが,粘性を無視した取扱いができる仮想的な流体を完全流体(perfect fluid)という。
また,一般に圧力によって流体の密度が変化するので圧縮性流体(compressible fluid)と呼ばれるが,流体の速度(圧力変化)が小さく,密度の変化が無視できる場合には非圧縮性流体(incompressible fluid)として扱われる。
液体と気体の明確な区別がなくなるような,臨界状態を超えた条件の下の流体を超臨界流体(supercritical fluid)という。
流体のせん断応力とせん断変形速度(流れの速度勾配,ずり速度)に比例関係があるとき,その流体はニュートン流体(Newtonian fluid)といい,比例関係にない流体を非ニュートン流体(Non-Newtonian fluid)という。非ニュートン流体には,せん断応力とせん断変形速度の関係により,ダイラタント流体,擬塑性流体,ビンガム流体などがある。
これらの流体に関する分類は,物体の力学的な挙動を議論するために導入された分類であり,物質の三態(固体・液体・気体)の概念とはかならずしも一致しない。
ページの先頭へ
【流体力学とは】
連続体力学(continuum mechanics)の一部と見なされることもあり,静止状態を扱う流体静力学(fluid statics),運動状態を扱う流体動力学(fluid dynamics)に分かれる。工学分野では,水を対象とする水力学(水理学),空気を対象とする空気力学にも分けられる。
流体力学では電気的に中性で電離していない流体のみを扱い,電離した流体は流体力学とは別分野とされるプラズマ物理学で扱われる。
流体静力学は,紀元前 220年アルキメデスの原理,1653年パスカルの原理,1662年ボイルの法則(ボイル・マリオットの法則)など,古くから発展してきた。
流体動力学は,ベルヌーイ,オイラー,ラグランジュらにより,ニュートン力学を完全流体に適用することで発展してきた。粘性流体については,19世紀に入ってからナビエ,ストークス,レイノルズらの研究により進んだ分野である。
流体力学に貢献した学者
● アルキメデス(紀元前287年頃~212年)
古代ギリシアの数学者,物理学者,技術者,発明家,天文学者。「てこの原理」や浮力の大きさは物体の排除した流体に働くべき重力に等しいという「アルキメデスの原理」の発見,投石機や揚水装置(アルキメデスの螺旋)などの機械類の発明,円周率の近似値を求めるなど多方面で活躍した。
● ブレーズ・パスカル(1623年~1662年)
フランスの哲学者,自然哲学者,思想家,数学者,キリスト教神学者。近代的物理学の先駆者。
● ロバート・ボイル(1627年~1691年)
アイルランド・リズモア出身の貴族,自然哲学者,化学者,物理学者,発明家。ボイルの法則で知られている。
● ダニエル・ベルヌーイ(1700年~1782年)
スイスの数学者・物理学者。1738年に『流体力学』を出版。ベルヌーイの定理「空気や水の流れがはやくなると,そのはやくなった部分は圧力が低くなる。はやく流れるほど圧力は下がる。」など,流体力学の基礎を築いた。
● レオンハルト・オイラー(1707年~1783年)
ロシア・ドイツの数学者・天文学者(天体物理学者)。オイラーの公式,オイラーの等式,オイラー積分など,微分積分の創始以来で,解析学の技法的な完成に寄与した。
● ジョゼフ=ルイ・ラグランジュ(1736年~1813年)
フランスの数学者,天文学者。オイラーと並ぶ18世紀最大の数学者。微分積分学の物理学,最小作用の原理に基づく解析力学(ラグランジュ力学)を作る。
● クロード・ルイ・マリー・アンリ・ナヴィエ(1785年~1836年)
フランスの数学者,物理学者。流体力学における基礎方程式(ナビエ–ストークス方程式)として知られる。
● サー・ジョージ・ガブリエル・ストークス(1819年~1903年)
アイルランドの数学者,物理学者。 ストークスの式,粘度など単位,ストークス散乱などで知られる。
● オズボーン・レイノルズ(1842年~1912年)
アイルランド生まれのイギリスの物理学者。レイノルズ数,レイノルズの輸送定理などで知られる。
● ルートヴィヒ・プラントル(1875年~1953年)
ドイツの物理学者。空気力学における境界層,薄翼の理論,揚力線理論などで知られる。
ページの先頭へ
【静止流体の圧力】
静止している流体では,設定した面に対して法線方向に垂直応力(圧力)が働き,接線方向の力は働かない。
ここで,下図に示すように,静止している流体中の任意の箇所に微小な三角錐(四面体)を想定し,三角錐の各面に対し,y・z 面(面積△OBC)に px ,x・z 面(面積△OCA)に py ,x・y 面(面積△OAB)に pz ,x・y・z 面(面積△ABC)に p の圧力が作用していると仮定する。
想定した三角錐の流体が静止しているので,各面に作用する力は,釣り合った状態にある。すなわち,各面の力は各面の面積に圧力をかけた値となる。
なお,力の釣り合いを考える場合は,x・y・z 面(△ABC)に作用する力をx 軸,y 軸,z 軸方向に分ける(ベクトルの座標変換)必要がある。
このため,面△ABC の外向きの法線の方向余弦(direction cosine)を( l , m , n )としたとき,各面の面積には
l・△ABC=△OBC ,m・△ABC=△OCA ,n・△ABC=△OAB
の関係があるので,これを用いる。
X 軸方向の力の釣り合い
px △OBC - p △ABC× l = 0
Y 軸方向の力の釣り合い
py △OCA - p △ABC×m = 0
Z 軸方向の力の釣り合い
Z 軸方向の圧力 pz による力のつり合いでは,三角錐の重力の影響が加わるので,流体の密度ρ,重力加速度 g ,三角錐の体積 V = (OA×OB×OC)÷6 とした時,
pz △OAB - p △ABC×n - ρg V = 0
とできる。
次いで,OA ,OB ,OC を限りなく小さくしてゆくと,三角錐の体積が無視できるほどに限りなく小さくなるので,点 O での圧力の大きさは,想定した 4 つの面の選び方(方向)に関係なく,
px = py = pz = p
となる。これをその点の静圧ともいう。

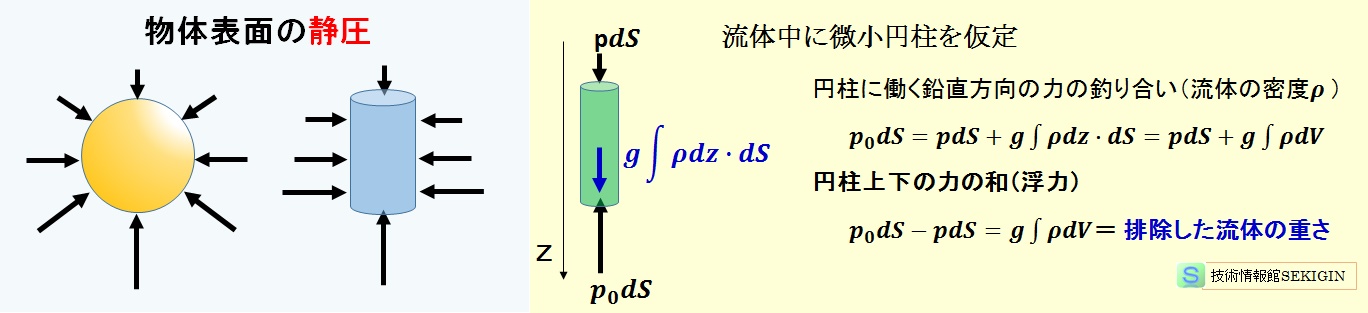
静止流体の圧力
ページの先頭へ
【アルキメデスの原理】
アルキメデスの原理(Archimedes' principle)とは,紀元前 220年にアルキメデスが発見した “静止状態の流体中の物体は,その物体が排除した流体の重さに等しい鉛直上向きの力を受ける” という原理である。この押上げる力を浮力(buoyancy)という。
静止流体中の物体と流体との境界面に対し垂直な静圧(static pressure)を及ぼす。この静圧の境界面について総和したものが浮力となる。
重力場では,流体の密度ρ( kg・m-3 ),物体の流体に浸っている部分の体積 V( m3 ),重力加速度 g( m・s‐2 )のとき,浮力 F は次式で与えられる。
F = -ρV g
式から分かるように,浮力の大きさは物体の密度には関係しない。
流体の密度より物体の質量/体積(平均密度や見かけの密度などという)が小さい場合には,物体の一部が流体より上に突出する。この時,物体に作用する重力と浮力が釣り合う。すなわち,物体の質量を m とすると,
m g = ρV g ∴ m = ρV
が成り立つ。
以上より,アルキメデスの原理は,流体の密度のみが反映し,流体の種類,物体の形状や材質には影響されないことが分かる。
アルキメデスの原理
ページの先頭へ
【パスカルの原理】
パスカルの原理(Pascal's principle)とは,1653年にブレーズ・パスカルが発見した“密閉した容器内で静止している非圧縮性流体の1点で圧力の増加があると,流体内のすべての点で同じ大きさの圧力の増加がみられる” という流体静力学における基本原理である。
密封容器中のある一点に外部から力が働き圧力が⊿p 増加した時,元の圧力が異なっていても,他のあらゆる点の圧力も同じ大きさの⊿p だけ増加する。
例えば,ペットボトルに水を満たし,ペットボトルの一部を指で押すなどして,応力(指の面積×加えた力)を加えた時,押す場所によらず,ペットボトル内の水の圧力は,あらゆる点で加えた応力と同じ大きさの圧力が増加する。
デカルトが発明したと言われている浮沈子(Cartesian diver)は,内部に空間を持ち,下端が小さく開いた小さな容器である。浮沈子の内部に水と空気を入れ,大気圧で僅かに浮くように浮力を調整したものを,水で満たし密封容器(ペットボトルなど)に入れ,容器に外から応力を加えることで沈み(diving),応力を開放することで浮く玩具である。これは,パスカルの原理とアルキメデスの原理を利用した玩具で,理科実験にも利用されている。
ページの先頭へ
【ボイルの法則】
1662年にロバート・ボイルにより,“一定温度で,一定量の気体の体積 V は圧力 P に反比例する”ことを主張するボイルの法則(Boyle's law)は,理想気体で成立する近似法則であり,実在気体の高い圧力領域では補正が必要になる。
1778年にジャック・アレクサンドル・セザール・シャルルが提唱した “圧力が一定のとき,理想気体の体積は熱力学(的)温度に比例する”ことを主張するシャルルの法則( Charles's law )とボイルの法則を合わせたボイル・シャルルの法則“気体の圧力 P は体積 V に反比例し,熱力学(的)温度 T に比例: PV / T = 一定” が気体の状態方程式(equation of state)として広く用いられている。
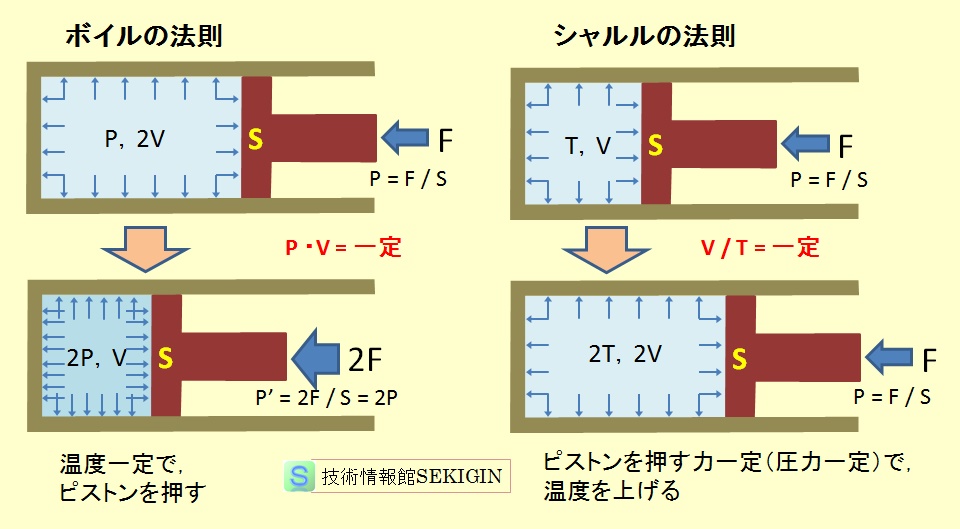
ボイルの法則とシャルルの法則のイメージ図
ページの先頭へ