腐食概論:腐食の基礎
☆ “ホーム” ⇒ “腐食・防食とは“ ⇒ “腐食概論(腐食の基礎)” ⇒
ここでは,腐食と化学反応に関連し, 【化学反応の速度定数とは】, 【主な用語】 を紹介する。
腐食は化学反応
化学反応の速度定数とは
鉄鋼は,鉄酸化物や鉄硫化物として存在する鉄鉱石を原料として,これにエネルギーを与えて還元することで得られる。このように,貴金属など一部の金属を除き,多くの金属は,酸化状態の化合物にエネルギーを与えて製造される。
すなわち,多くの金属は,原料とした酸化物より化学ポテンシャル(chemical potential)の高い状態,言い換えれば熱力学的には不安定な状態にあることを示す。
しかしながら,リチウム(Li),ナトリウム(Na),カリウム(K)などのアルカリ金属やカルシウム(Ca)などのアルカリ土類金属など一部の金属を除き,多くの金属は,熱力学的に不安定ではあるが,実用上で不都合なく利用(物質として安定)されている。
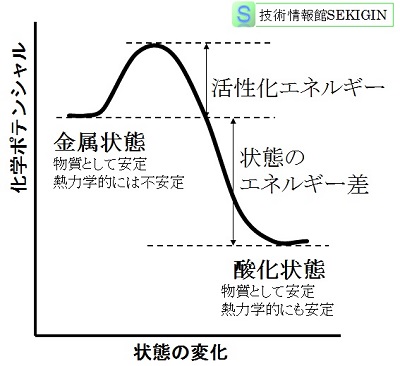
金属の状態変化とエネルギー(概念図)
図に示すように,状態変化には超えなければならない壁{活性化エネルギー(activation energy)}が存在する。
実用金属は,活性化エネルギーを容易に超えない環境で使用されている限り,実用期間中に大きな状態変化に至らない。
しかし,温度の上昇,活性化エネルギーの小さい中間経路の経由などの環境変化で,活性化エネルギーを容易に超えるような状況にさらされると,比較的早い期間に熱力学的に安定な酸化状態に変化し,状態のエネルギー差に相当する熱を放出(発熱反応)し自発的に反応が継続する。例えば,使い捨てカイロ(鉄粉+塩+おがくず+水+酸素)は,この熱を有効利用した製品である。
状態変化の速さ,すなわち化学反応の速さは,反応に関わる物質の濃度(活量; activity)と反応速度式の速度定数(rate constant)に比例する。なお,速度定数は,次式のアレニウスの式(Arrhenius equation)で示されるように,活性化エネルギーと温度に依存する。
アレニウスの式 : k=A e-Ea/RT
ここに,k:反応速度定数,A:頻度因子,e:自然対数の底(ネイピアの数),
Ea:活性化エネルギー,R:気体定数,T:絶対温度
ページのトップへ
主な用語の概説
アレニウスの式(Arrhenius equation)
1884年にスウェーデンのスヴァンテ・アレニウスが提唱した化学反応の速度を予測する式である。活性化エネルギーはアレニウスパラメータとも呼ばれる。
活性化エネルギー(activation energy)
反応物のエネルギー状態が基底状態から,遷移状態に励起するのに必要なエネルギーをいう。
遷移状態(せんいじょうたい;transition state)とは,化学反応で反応物から生成物に変わる過程で通る最もエネルギーの高い状態を遷移状態という。
活量(activity)
ある成分の化学ポテンシャルに関連して与えられる一種の熱力学的濃度(JIS K 0213 参照)。【 JIS K 0211「分析化学用語(基礎部門)」】
理想系と実在系に存在する誤差を修正するためにギルバート・ルイスによって導入された物理量。
(相対)活量 a i = exp { ⊿μi / RT } ここに,μi:i 成分の化学ポテンシャル,R:気体定数,T:熱力学的温度 【 JIS K 0213「分析化学用語(電気化学部門)」】
活量は,アメリカの物理化学者,ギルバート・ニュートン・ルイス( 1875 ~ 1946 年)によって導入された物理量で,a で表され,活動度とも呼ばれる。
活量係数(activity coefficient)
aB / XB aB / ( mB / M0 ) 又は aB / ( CB / C0 ) で定義される数値。
ここに,aB :成分 B の相対活量, XB ,mB ,及び CB:それぞれ成分 B のモル分率,質量モル濃度,及びモル濃度, M0 ,及び C0 :それぞれ標準質量モル濃度(通常,1 mol / kg )及び標準モル濃度(通常,1 mol / L )【 JIS K 0213「分析化学用語(電気化学部門)」】
理想とする数値からのずれを表す指標として,活量係数(activity coefficient)が定義され,I 成分の活量 ai ,モル分率χi ,活量係数γi の間には次の関係にある。
ai = γi ・χi
化学ポテンシャル(chemical potential)
ギブズにより導入された浸透圧や化学反応のようなマクロな物質量の移動が伴う現象で重要な示強性状態量の一つである。混合物中に存在する一つの成分 1 モル当たり,又は 1 分子当たりのギブズエネルギーに相当する。
ギブズエネルギー(Gibbs energy)
ギブズの自由エネルギーともいわれ,熱力学や電気化学などで用いられ,等温等圧条件下で仕事として取り出し可能なエネルギーを表す示量性状態量である。ギブズエネルギー G は,G = H - T S (ここで,H :エンタルピー ,T :熱力学温度,S :エントロピー )と定義される。
示量状態量(extensive property)
読み「しりょうじょうたいりょう」,示量変数(extensive variable)ともいわれ,系内の物質の量に比例する状態量をいう。例えば,体積,物質量,質量,エントロピー,エンタルピーがが挙げられる。
示強状態量(intensive property)
読み「しきょうじょうたいりょう」,示強変数(intensive variable)ともいわれ,物質の量に依存しない状態量をいう。例えば,圧力,温度,密度,濃度,エントロピー,化学ポテンシャルが挙げられる。
ページのトップへ